mathglpp::LinearPolynomial< T > Class Template Reference

Collaboration diagram for mathglpp::LinearPolynomial< T >:

[legend]List of all members.

---

Detailed Description

template<typename T = double>
class mathglpp::LinearPolynomial< T >

Definition at line 39 of file LinearPolynomial.h.

Public Member Functions
	LinearPolynomial (size_t size)
	LinearPolynomial (const T &val, size_t size)
	LinearPolynomial (const T *p, size_t size)
	LinearPolynomial (const LinearPolynomial &lp)
	~LinearPolynomial ()
T	rem () const
size_t	size () const
T &	operator[] (size_t ind)
T	evaluate (T x) const
T	operator() (T x) const
LinearPolynomial &	operator= (const LinearPolynomial &lp)
LinearPolynomial	operator+ (const LinearPolynomial &lp) const
LinearPolynomial &	operator+= (const LinearPolynomial &lp)
LinearPolynomial	operator- (const LinearPolynomial &lp) const
LinearPolynomial &	operator-= (const LinearPolynomial &lp)
LinearPolynomial	operator * (T val) const
LinearPolynomial &	operator *= (T val)
LinearPolynomial	operator * (const LinearPolynomial &lp) const
LinearPolynomial &	operator *= (const LinearPolynomial &lp)
LinearPolynomial	operator/ (T val) const
LinearPolynomial &	operator/= (T val)
LinearPolynomial	operator/ (const LinearPolynomial &divisor) const
LinearPolynomial &	operator/= (const LinearPolynomial &divisor)
bool	Newton_Raphson (const LinearPolynomial &derivative, T &sample, T threshold=0.00000000001, int cutoff=40)
	returns true if the root is found
bool	quadratic_formula (T &root1, T &root2)
	returns false if the roots are complex, then root1 will be the median and root2 the discriminant otherwise the positive root is root1 and the negative root is root2, that is positive and negative translation from the median -b/2a.
std::vector< T >	findRoots (void)
LinearPolynomial	derivate (void)
LinearPolynomial	integrate_with_root (T x_root)
LinearPolynomial	integrate_with_origin (T y_origin)
Protected Attributes
std::valarray< T >	fx
T	remainder
Friends
template<class _CharT, class _Traits>
std::basic_ostream< _CharT, _Traits > &	operator<< (std::basic_ostream< _CharT, _Traits > &out, const LinearPolynomial &lp)

---

Member Function Documentation

template<typename T = double>

bool mathglpp::LinearPolynomial< T >::Newton_Raphson	(	const LinearPolynomial< T > &	derivative,
		T &	sample,
		T	threshold = 0.00000000001,
		int	cutoff = 40
	)			[inline]

returns true if the root is found

Definition at line 246 of file LinearPolynomial.h.

References mathglpp::LinearPolynomial< T >::evaluate(), mathglpp::LP_almost_zero(), and mathglpp::LP_new_sample().

Referenced by mathglpp::LinearPolynomial< T >::findRoots().

    {
        //choose a sample point
        T root;
        T gradient = T(1);
        int i;

        for(i = 0; i < cutoff; ++i)
        {
            root = evaluate(sample);
            //std::cout << "root: "<< root <<", \tat: "<< sample << ", threshold: " << threshold << endl;
            if( LP_almost_zero(root,threshold) )
                break;//root found

            //find a guaranteed root as long as the gradient is not close to 0
            gradient = derivative.evaluate(sample);

            while( LP_almost_zero(gradient, T(0.0000001)) )
            {
                LP_new_sample(sample);
                gradient = derivative.evaluate(sample);
            }

            //recalculate sample position
            sample = sample - root/gradient;
        }

        sample = -(sample);

        if(i == cutoff)//complex roots, probably...
            return false;
        else
            return true;
    }

Here is the call graph for this function:

template<typename T = double>

bool mathglpp::LinearPolynomial< T >::quadratic_formula	(	T &	root1,
		T &	root2
	)			[inline]

returns false if the roots are complex, then root1 will be the median and root2 the discriminant otherwise the positive root is root1 and the negative root is root2, that is positive and negative translation from the median -b/2a.

Definition at line 284 of file LinearPolynomial.h.

References mathglpp::LinearPolynomial< T >::fx.

Referenced by mathglpp::LinearPolynomial< T >::findRoots().

    {
        //x = (-b +/- sqrt(b^2 - 4ac))/2a
        bool non_complex = true;
        T b = fx[1];
        T a2 = 2*fx[2];
        T c = fx[0];
        T discriminant = b*b - 2*a2*c;
        if( discriminant < T(0) )
        {
            non_complex = false;
            root1 = -b/a2;
            root2 = discriminant;
        }
        else
        {
            T sqrtDisc = sqrt(discriminant);
            root1 = -b/a2 + sqrtDisc;
            root2 = -b/a2 - sqrtDisc;
        }

        return non_complex;
    }

template<typename T = double>

std::vector<T> mathglpp::LinearPolynomial< T >::findRoots

(

void

)

[inline]

we should really do some complex root checking here

Definition at line 308 of file LinearPolynomial.h.

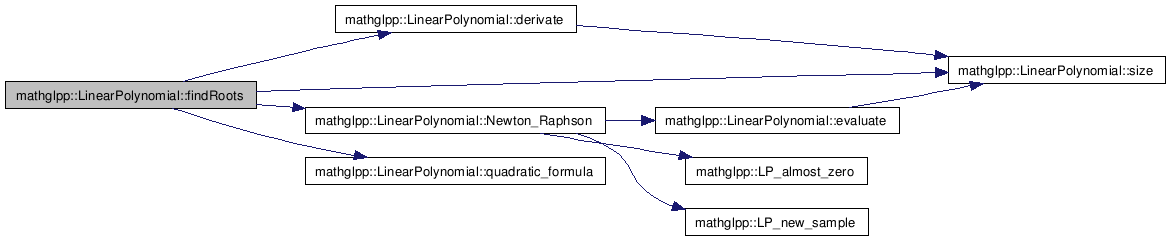
References mathglpp::LinearPolynomial< T >::derivate(), mathglpp::LinearPolynomial< T >::Newton_Raphson(), mathglpp::LinearPolynomial< T >::quadratic_formula(), and mathglpp::LinearPolynomial< T >::size().

Referenced by mathglpp::GLMatrix< value_type >::eigenValues().

    {
        LinearPolynomial temp(*this);
        LinearPolynomial derivative(*this);

        std::vector<T> retval;
        retval.resize(size()-1);
        T root[] = { 0, 1 };
        register int i;

        for(i = 0; temp.size() > 3; ++i)
        {
            derivative = temp.derivate();
            temp.Newton_Raphson(derivative,root[0]);
            retval[i] = -root[0];
            //std::cout<<"root[]: "<<root[0]<<", "<<root[1]<<endl;
            //std::cout<<"temp, before: "<<temp;
            LinearPolynomial lp(root,2);
            //std::cout<<"divisor: "<<lp;
            temp /= lp;
            //std::cout<<"temp, after: "<<temp;
        };

        if(temp.size() > 2)
        {
            temp.quadratic_formula(retval[i], retval[i+1]);
        }
        else
            retval[i] = -temp[0];

        return retval;
    }

Here is the call graph for this function:

---

The documentation for this class was generated from the following file:

• LinearPolynomial.h

---