mathglpp::GLPlane< T > Class Template Reference

Collaboration diagram for mathglpp::GLPlane< T >:

[legend]List of all members.

---

Detailed Description

template<typename T>
class mathglpp::GLPlane< T >

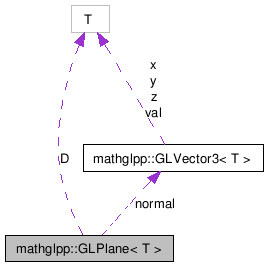
Definition at line 38 of file GLPlane.h.

Public Types
typedef GLVector3< T >	vector_type
	Typedef it so that the class is more resilient to change.
Public Member Functions
	GLPlane ()
	Construct a zero plane, for convenience mainly.
	GLPlane (const vector_type &n, const vector_type &op)
	Construct a directed plane, with a translation so that op is on the plane.
	GLPlane (const vector_type &op1, const vector_type &op2, const vector_type &op3)
	Construct a directed plane, so that op[1,2,3] are on the plane.
	GLPlane (const GLPlane &pl)
	Normal copy constructor.
	~GLPlane ()
	Normal destructor.
void	set (const vector_type &op1, const vector_type &op2, const vector_type &op3)
	3 point mutator, the three points for a plane
const vector_type &	getNormal (void) const
	Simple const accessor, normal.
void	setNormal (const vector_type &n)
	Simple mutator, normal.
const T &	getD (void) const
	Simple const accessor, deflection.
void	setD (const T &d)
	Simple mutator, deflection.
T	distanceToPoint (const vector_type &p) const
	Use this to find out how far away from the plane a point is.
T	intersectionWithLine (const vector_type &dir, const vector_type &origin) const
	Use this to find out how far along the line the plane is intersected.
vector_type	reflectedVector (const vector_type &in) const
	Use this to get a plane reflected vector.
GLMatrix< T >	reflectionMatrix ()
	Get a plane reflection matrix from the plane equation.
GLMatrix< T >	directionalProjectionMatrix (const vector_type &dir)
	Get an orthogonal projection matrix. Useful for simple shadows and other casting.
GLMatrix< T >	pointProjectionMatrix (const vector_type &l)
	Point perspective projection of vertecies with respect to a projection source, useful for shadow projections.

---

Member Typedef Documentation

template<typename T>

typedef GLVector3<T> mathglpp::GLPlane< T >::vector_type

Typedef it so that the class is more resilient to change.

Definition at line 42 of file GLPlane.h.

---

Constructor & Destructor Documentation

template<typename T>

mathglpp::GLPlane< T >::GLPlane

(

)

[inline]

Construct a zero plane, for convenience mainly.

Definition at line 45 of file GLPlane.h.

    :normal(T(0)),D(T(0))
    {}

template<typename T>

mathglpp::GLPlane< T >::GLPlane	(	const vector_type &	n,
		const vector_type &	op
	)			[inline]

Construct a directed plane, with a translation so that op is on the plane.

Definition at line 50 of file GLPlane.h.

    :normal(n), D(-(n.dot(op))) {}

template<typename T>

mathglpp::GLPlane< T >::GLPlane	(	const vector_type &	op1,
		const vector_type &	op2,
		const vector_type &	op3
	)			[inline]

Construct a directed plane, so that op[1,2,3] are on the plane.

Definition at line 54 of file GLPlane.h.

References mathglpp::GLVector3< T >::dot(), and mathglpp::GLVector3< T >::normalize().

    { normal = (op3 - op2).getCross( (op1 - op2) );  normal.normalize(); D = -(normal.dot(op1)); }

Here is the call graph for this function:

template<typename T>

mathglpp::GLPlane< T >::GLPlane

(

const GLPlane< T > &

pl

)

[inline]

Normal copy constructor.

Definition at line 58 of file GLPlane.h.

: normal(pl.normal), D(pl.D) {}

template<typename T>

mathglpp::GLPlane< T >::~GLPlane

(

)

[inline]

Normal destructor.

Definition at line 61 of file GLPlane.h.

{}

---

Member Function Documentation

template<typename T>

void mathglpp::GLPlane< T >::set	(	const vector_type &	op1,
		const vector_type &	op2,
		const vector_type &	op3
	)			[inline]

3 point mutator, the three points for a plane

Definition at line 64 of file GLPlane.h.

References mathglpp::GLVector3< T >::dot(), mathglpp::GLVector3< T >::getCross(), and mathglpp::GLVector3< T >::normalize().

    { normal = (op3 - op2).getCross( (op1 - op2) );  normal.normalize(); D = -(normal.dot(op1)); }

Here is the call graph for this function:

template<typename T>

const vector_type& mathglpp::GLPlane< T >::getNormal

(

void

)

const [inline]

Simple const accessor, normal.

Definition at line 68 of file GLPlane.h.

    { return normal; }

template<typename T>

void mathglpp::GLPlane< T >::setNormal

(

const vector_type &

n

)

[inline]

Simple mutator, normal.

Definition at line 72 of file GLPlane.h.

    { normal = n; }

template<typename T>

const T& mathglpp::GLPlane< T >::getD

(

void

)

const [inline]

Simple const accessor, deflection.

Definition at line 76 of file GLPlane.h.

    { return D; }

template<typename T>

void mathglpp::GLPlane< T >::setD

(

const T &

d

)

[inline]

Simple mutator, deflection.

Definition at line 80 of file GLPlane.h.

    { D = d; }

template<typename T>

T mathglpp::GLPlane< T >::distanceToPoint

(

const vector_type &

p

)

const [inline]

Use this to find out how far away from the plane a point is.

Definition at line 84 of file GLPlane.h.

References mathglpp::GLVector3< T >::dot().

Referenced by mathglpp::GLPlane< T >::reflectedVector().

    { return (normal.dot(p) + D); }

Here is the call graph for this function:

template<typename T>

T mathglpp::GLPlane< T >::intersectionWithLine	(	const vector_type &	dir,
		const vector_type &	origin
	)			const [inline]

Use this to find out how far along the line the plane is intersected.

Used for picking and simple raytracing mostly.

Definition at line 89 of file GLPlane.h.

References mathglpp::GLVector3< T >::dot().

    { return - (normal.dot(origin) + D) / normal.dot(dir); }

Here is the call graph for this function:

template<typename T>

vector_type mathglpp::GLPlane< T >::reflectedVector

(

const vector_type &

in

)

const [inline]

Use this to get a plane reflected vector.

Definition at line 93 of file GLPlane.h.

References mathglpp::GLPlane< T >::distanceToPoint().

    { return in - (normal*(distanceToPoint(in))*2); }

Here is the call graph for this function:

template<typename T>

GLMatrix<T> mathglpp::GLPlane< T >::reflectionMatrix

(

)

[inline]

Get a plane reflection matrix from the plane equation.

Definition at line 97 of file GLPlane.h.

References mathglpp::GLVector3< T >::x, mathglpp::GLVector3< T >::y, and mathglpp::GLVector3< T >::z.

    {
        GLMatrix<T> ret;

        ret[0] = 1 - 2*(normal.x*normal.x);
        ret[4] =   - 2*(normal.x*normal.y);
        ret[8] =   - 2*(normal.x*normal.z);
        ret[12] = -2*normal.x*D;

        ret[1] =   - 2*(normal.y*normal.x);
        ret[5] = 1 - 2*(normal.y*normal.y);
        ret[9] =   - 2*(normal.y*normal.z);
        ret[13] = -2*normal.y*D;

        ret[2] =   - 2*(normal.z*normal.x);
        ret[6] =   - 2*(normal.z*normal.y);
        ret[10] = 1  - 2*(normal.z*normal.z);
        ret[14] = -2*normal.z*D;

        ret[3] = 0;
        ret[7] = 0;
        ret[11] = 0;
        ret[15] = 1;

        return ret;
    }

template<typename T>

GLMatrix<T> mathglpp::GLPlane< T >::directionalProjectionMatrix

(

const vector_type &

dir

)

[inline]

Get an orthogonal projection matrix. Useful for simple shadows and other casting.

Definition at line 125 of file GLPlane.h.

References mathglpp::GLVector3< T >::x, mathglpp::GLVector3< T >::y, and mathglpp::GLVector3< T >::z.

    {
        GLMatrix<T> ret;

        ret[0] = 1+1*(dir.x*normal.x);
        ret[4] =   1*(dir.x*normal.y);
        ret[8] =   1*(dir.x*normal.z);
        ret[12] =  1*dir.x*D;

        ret[1] =   1*(dir.y*normal.x);
        ret[5] = 1+1*(dir.y*normal.y);
        ret[9] =   1*(dir.y*normal.z);
        ret[13] =  1*dir.y*D;

        ret[2] =   1*(dir.z*normal.x);
        ret[6] =   1*(dir.z*normal.y);
        ret[10] =1+1*(dir.z*normal.z);
        ret[14] =  1*dir.z*D;

        ret[3] = 0;
        ret[7] = 0;
        ret[11] = 0;
        ret[15] = 1;

        return ret;
    }

template<typename T>

GLMatrix<T> mathglpp::GLPlane< T >::pointProjectionMatrix

(

const vector_type &

l

)

[inline]

Point perspective projection of vertecies with respect to a projection source, useful for shadow projections.

Definition at line 153 of file GLPlane.h.

References mathglpp::GLVector3< T >::dot(), mathglpp::GLVector3< T >::x, mathglpp::GLVector3< T >::y, and mathglpp::GLVector3< T >::z.

    {
        GLMatrix<T> ret;

        T d = -l.dot(normal);
        T c = D - d;

        ret[0] = -l.x*normal.x + c;
        ret[4] = -l.x*normal.y;
        ret[8] = -l.x*normal.z;
        ret[12]= -c*l.x - d*l.x;

        ret[1] = -l.y*normal.x;
        ret[5] = -l.y*normal.y + c;
        ret[9] = -l.y*normal.z;
        ret[13]= -c*l.y - d*l.y;

        ret[2] = -l.z*normal.x;
        ret[6] = -l.z*normal.y;
        ret[10] = -l.z*normal.z + c;
        ret[14]= -c*l.z - d*l.z;

        ret[3] = -normal.x;
        ret[7] = -normal.y;
        ret[11] = -normal.z;
        ret[15]= -d;

        return ret;
    }

Here is the call graph for this function:

---

The documentation for this class was generated from the following file:

• GLPlane.h

---